Использование априорной информации для сокращения объема испытаний

14.2.1. Байесовский метод оценивания

В процессе проектирования сложных систем в результате проведения теоретических расчетов, математического и полунатурного модели­рования, различного вида испытаний, а также использования опыта проектирования аналогичных изделий накапливается значительная информация о надежности и эффективности разрабатываемого изде­лия.

668

Таблица 14.1 Зависимость оценок показателей эффективности системы от оценок показателей эффективности подсистем Математи­ ческая модель Оценка показателей эффективности подсистем Оценка показателей эффективнос­ти системы Доверительный интервал Объем испытаний автономный подход системный ПОДХОД 1 2 3 4 5 6 1. Вероят­ность без­отказной работы Л = П*. 1=1 d: Я, = 1—- 1- щ *=m /=і ^вОЬкв» ^ЭКВ* У) *н (^экв » ^ЭКВ » у) «экв =тіп{лІ} ^ЭКВ = “ ^ЭКВ^} R3=0,9 У = </ = я,- = 293 Л,, =0,99 0,95 = 0 ", min = 29 2. Интен­сивность отказов л = І>, 1=1 Планы NU(M) Т Ї-І = п/% Планы [NU(M)r] Ъ = (г« -1)/% >>  и ЇМ*- -Г Планы [NU(M)7] ( к (к > Х(1-у)/2 Х(1+у)/2 2^J/+2 I=1 I ^ к ^ *=1 ; Л3 = о, 1 У = г = ty min = 370 2*П11П X, =0,01 0,95 = 0 ty • = 37 2, min ^Imax ^Imin Планы [Л^6Г(Л0»1 ( к ( к Х(1-у)/2 Х(1+у)/2 —————— ———- LizL-j ^Lmax ^Lmin

os о	Окончание табл. 14.1 1 2 3 4 5 6 3. Диспер­сия а2=Іа? 1=1 5/= Д(*« "»■1 І-1 s2=ts? 1=1 Х(Щ)/2(у) X(1-y)/2 (v) [І**/2] v — w 1 о, равны щ равны ‘ Хр(я( -1) a = f n = 5 Ki =13,3; 5; 2,9 r..Х?-а(*л/-*) L Xp (*«/-*) 1 = 0,05 10; 20 ^£ = 2,1; 1,8; 1,5 к min (л,- -1) £ v £ XO1! “ 1) i=l 4. Среднее значение к М = i=l й.-1 Іч "і <=1 -WS и Л — г,_^2 (я — l)s2 (w ) ^ M 5 S M +/j_0^2(w-1)S2(w ) а, равны щ равны *l-a/2 V — V — Г|1 I, , 1 4-a/2 41+2 n-1 a = f 6/a = л =15; 55 1 = 0,05 = 3; 1,2 n = 5; 10

 

К сожалению, эта информация разнородна, т. е. оцениваются различные показатели эффективности как подсистем, так и системы в целом, измерения параметров и характеристик системы произво­дятся с различной точностью, испытания осуществляются в различ­ных условиях и пр. Все это затрудняет использование имеющейся обширной априорной информации и требует разработки математи­ческих методов получения комбинированных (объединенных) оце­нок показателей надежности и эффективности изделий.

Байесовский метод оценивания основан на использовании наи­более полной априорной информации об оцениваемом показателе R в виде априорного распределения неизвестного оцениваемого параметра P(R) и плотности распределения измеряемых характе­ристик как функции неизвестного показателя (функция правдопо­добия) P(x/R) [25].

Метод базируется на формуле Байеса, котрая позволяет опреде­лить апостериорную плотность вероятности неизвестного показателя P(R/x), являющуюся наиболее полной характеристикой оценки R и содержащую как априорную, так и статистическую информацию.

Согласно этой формуле апостериорная плотность вероятности:

пт-™™*.

где Р(х) = J P{R)P(x/R)dR — безусловная плотность вероятности из — п

мерений; Q — область задания показателя R.

Общей характеристикой точности байесовских оценок является средний риск. Для вычисления среднего риска необходимо задаться функцией потерь, которая в общем случае является некоторой функ­цией оценки и истинного значения оцениваемого показателя. Наиболее распространенными функциями потерь являются:

Л Л

• простая функция потерь Tl(R, R) = C-S(R-R), где константа 0 0,8 — дельта-функция;

АЛА

• квадратичная функция потерь П(Л, R) = (R-R) ;

А

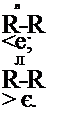функция потерь, равная модулю ошибки П(Л, R) =

Среднее по всевозможным выборкам значение функции потерь носит название условного риска:

оо

r(R)= J П(Л, R)P(x/R)dx.

—ОО

Средний риск получается усреднением условного риска по всевоз­можным значениям оцениваемого параметра:

tV = j r(R)P(R)dR. а

В качестве байесовских оценок могут быть приняты различные характеристики апостериорного распределения, которые минимизи­руют средний риск при той или иной функции потерь. Такими наи­более распространенными характеристиками являются мода, медиа­на и математическое ожидание апостериорной плотности вероятности.

Апостериорная мода минимизирует средний риск при простой функции потерь. Эта оценка обладает свойствами, аналогичными свойствам хорошо известной и широко используемой в практике ста­тистического анализа оценки максимального правдоподобия. Апос­териорная медиана минимизирует средний риск при функции потерь, равной модулю ошибки. Апостериорное математическое ожидание минимизирует средний риск при квадратичной функции потерь. Минимальный средний риск при этом равен дисперсии оцениваемо­го параметра.

Действительно, средний риск при квадратичной функции потерь запишется как

оо

W = f f (R-R)2P(R)P(x/R)dRdx

£2-оо

ИЛИ

оо

W = f J (R-R)2P(R/x) Р(х) dRdx =

£2-оо

оо

= J ЇМ2 [R/ х]+D[R/x]-2M[R/x]R+R2~P(x)dx.

При выборе R = M[R/x получим выражение для минимального среднего риска:

ОО

W= j D[R/x]P(x)dx = D[x].

—ОО

Для унимодальной и симметричной апостериорной плотности вероятности все три приведенные оценки совпадают. В’частности, это имеет место при нормальном распределении.

При несовпадении указанных оценок чаще всего применяют апо­стериорное математическое ожидание, что объясняется в основном более простой вычислительной процедурой построения оценки M[R/х] и определения ее точности. Кроме того, эту оценку называют оцен­кой равного риска, так как при выборе R = М [Л/х] вероятности зна­чений R, больших и меньших Д одинаковы. Поэтому апостериорное математическое ожидание в качестве оптимальной байесовской оценки не дает предпочтения ошибкам в зависимости от их величины. При необходимости придания большей значимости малым ошибкам ис­пользуется мода, а большим ошибкам — медиана.

‘ При практическом использовании байесовских оценок априор­ное распределение P(R) чаще всего определяют на основе обработки данных испытаний изделий-аналогов. Это так называемый эмпири­ческий байесовский подход. Опишем типичную ситуацию для эф­фективного применения данного подхода. Пусть по результатам ис­пытаний некоторого изделия получена оценка исследуемого показателя Д. По результатам испытания второго изделия получена оценка ана­логичного показателя Д. Вследствие действия рада неучтенных слу­чайных факторов оценка Д отлична от Д. Другими словами, суще­ствует диапазон возможных значений параметра R, в котором он изменяется случайным образом. Неопределенность в значениях R можно описать априорной плотностью вероятности P(R). Заметим, что при рассмотрении задач такого рода необходимо исключить изме­нение показателя по какому-либо неслучайному закону. Ниже при­водится методика эмпирического байесовского подхода [16].

В соответствии с формулой Байеса имеем:

PjxJR)

J P(R)P(Xl/R)dR ’ n

где Xj — некоторое выборочное значение из распределения P(x/R).

P(x2/R)

jP(R/Xl)P(x2/R)dR’

Cl где x2 — следующее выборочное значение x, независимое от *j, а полученная ранее плотность распределения P(R/xj) используется в качестве нового априорного распределения.

3. По известной выборке {х1?…, хл} при помощи 5-функций стро­ится эмпирическое распределение

W = — S «<*>*/)•

пы

4. На основе использования равенства Рэ(х) = J P{Rjx)P3{x)dR

сі

строится эмпирическое априорное распределение

P3(R) = — fJg(R, xi),
пы

где g(R, jc) = [/* (Л/jc)] — ядро, обратное P(x/R).

Таким образом, усилия, связанные с преодолением априор­ной неопределенности, сводятся к решению интегрального уравне­ния относительно P3(R) .

Помимо статистических данных априорное распределение мо­жет строиться на основе данных экспертных оценок: оно представля­ет собой в этом случае субъективное распределение вероятностей. При отсутствии априорных данных, необходимых для построения априор­ного распределения, процедура построения оценки неизвестного по­казателя R может основываться на минимаксном критерии. Мини­максной называется оценка, для которой верхняя граница условного риска не превосходит верхних границ при любых других оценках.

Вальд доказал, что минимаксная оценка является байесовской оценкой при априорном распределении оцениваемого показателя, для которого средний риск имеет наибольшую величину [16] . Он пока­зал также, что байесовская оценка, для которой условный риск не зависит от R, является минимаксной. Однако это условие является необходимым, но не достаточным, и общего метода нахождения наи­менее благоприятного априорного распределения, к сожалению, не существует. В этой связи представляются чрезвычайно интересными результаты построения наименее благоприятных априорных распре­делений в смысле максимума энтропии [35].

Анализ данных результатов привел к практически важному выво­ду: все наименее благоприятные априорные распределения, обеспе­чивающие максимум энтропии, являются «самовоспроизводящими — ся» распределениями, т. е. распределениями, вид которых не меняется после коррекции на основе экспериментальных данных в соответствии с методом Байеса. Комбинация этого свойства с использованием эмпирического байесовского подхода позволяет построить удобную

инженерную методику определения априорных распределений, из­ложенную ниже.

1. Функция правдоподобия выражается через ядро, зависящее как от измерений х, так и от оцениваемого показателя R и соответ­ствующего нормирующего коэффициента, зависящего только от из­мерений х:

P(x/R) = K(x)f(x/R),

где К — нормирующий коэффициент, который определяется соотно­шением

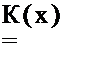1

jf(x/R)dR

а

2. Апостериорная плотность вероятности представляется в виде

P(R/x) = A(x)B(R)f(x/R),

где нормирующий коэффициент А(х) определяется соотношением

1

B(R)f(x/R)dR ■ а

Условие «самовоспроизводимости» может быть удовлетворено исходя из предположения представимости априорной плотности ве­роятности в виде P(R) = C(x)f(x/R), где в качестве ядра используется ядро функции правдоподобия f(x/R), а нормирующий коэффици­ент определяется как С(х) = jj f(x/R)dR.

3. В результате проведенных выкладок апостериорная плотность вероятности может быть представлена в виде

P(R/x) = K(x)f(x’/R)f(x/R) = K(x)f(x"/R),

где х означает априорные «измерения», полученные при испытани­ях изделий-аналогов; х" определяется покомпонентным сложением, а нормирующий коэффициент рассчитывается по формуле

Klx) = — f———— ————- .

jf(x’/R)f(x/R)dR

Q

Проиллюстрируем применение данной методики для ряда част­ных случаев, широко встречающихся в практике получения результа­тов испытаний.

Оценка математического ожидания нормального закона распре­деления при известной дисперсии. Наиболее просто байесовская оцен­ка строится для математического ожидания нормального распределе­ния в случае, когда известна дисперсия. Тогда функция правдоподобия имеет вид

Р (Xi9…,Xn/fflX9 ^х) “

= (2л)~"/2 ехр {- і hx (л -1) S2} exp j — і hxn (х — тх )2 } А*л/і,

mehx=l/a2x; * = -]►>,; Sx2 = ^£(х,—xf.

тт J1 /=1 /=1 ^

Для данной функции правдоподобия самовоспроизводящимся априорным законом распределения также является нормальное рас­пределение

Р(тх) = (2%) V2exp{—-*o)2}(V0)V2
с математическим ожиданием Mq [тх ] = xq и дисперсией Д) тх ] =

пределения Xq определяется как Хп =— Л. Х/. Используя формулу

«о»=1

Байеса, получим апостериорное нормальное распределение: P(mx/hx, xl,…,x„)=(2n)~lJ2 ехр{-^АхЛоб (тх — Хоб)2}(Моб)*,

где no6=nQ+n, хо6= (xq/Jq + хл)/(лд + л).

В качестве оценки математического ожидания принимаем апос­териорное математическое ожидание А/[ліх] *об* Точность этой оценки характеризуется апостериорной дисперсией Z)[/nx] = І/А^л^.

Проводя аналогичные выкладки, нетрудно получить байесовскую оценку математического ожидания тх при различных значениях дис­персий Од * о2, обусловленных, например, различием точностных характеристик средств измерений. В этом случае объединенная оценка имеет вид

*o/q2(x0) + x/a2 (де) 06 i/o2 (x0) + i/q2 (x) ’

а ее точность характеризуется дисперсией

Оценка дисперсии нормального закона распределения при извест­ном математическом ожидании. В том случае, если математичес­кое ожидание известно, а необходимо оценить дисперсию, функция правдоподобия записывается в виде:

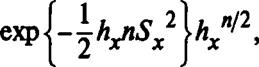P{xi>—>xn/mx>hx) — (2я)

гда sx = hf.{xi ~ mxf ■

Для данной функции правдоподобия самовоспроизводящимся априорным законом распределения является у-распределение 2-го рода:

с математическим ожиданием Л/q [А* ] = i/Sq и дисперсией Д) [А* ] =

= 2/яо^О2)2-

Апостериорное распределение представляет собой также у-рас — пределение 2-го рода:

У*об/2-1 I

P(hx/mx, xu…,xn) =

у

где «об = «о + ", ^об = (‘S’o «О + ^2«)/(«0+я)-

В качестве оценки неизвестной дисперсии принимаем апостери­орное математическое ожидание

M[ftx] = -^2~ ИЛИ MWx = Sdo-

Ооб

Лоб-

Р (x,…,Xn/mX9hx) — ~А*(л-1)52 — ivK*-mx)

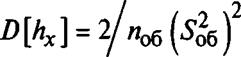
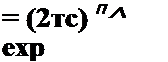Совместное оценивание математического ожидания и дисперсии нормального закона распределения. Наибольшую сложность представ­ляет случай совместного оценивания математического ожидания и дисперсии. Для этого случая функция правдоподобия имеет вид:

где х = — £ Xj; S2 = —|-г £ (х/ — xf (іп > 1); S2 = 0 (и = 1).

Л і 1% ” JL «

/=1 /=1

Для данной функции правдоподобия самовоспроизводящимся априорным законом распределения является гамма-нормальное рас­пределение

P(mx, hx) = (2п) 1/2 ехр{-^А*ло(л1х — д*>)2}х
х (Ах «О f2 ехр {- { fbcV0S$ }(1 A*v0 $ )V°/2 1 ^

с параметрами xq, щ, Sq, vq = щ -1.

Апостериорное совместное распределение представляет собой также у-нормальное распределение с параметрами

Хоб =(^)«о +хп)/(по+п) «об = «о + л; vo6 =Доб -1;

^0 («0 ~1) + ‘у2 (и-1) + (х-х0)2Яол/(яо +л)

«о +л-1

Апостериорным одномерным распределением являются:

(™Х — *об )2 *^об / об

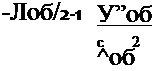• /-распределение Стьюдента для математического ожидания

с математическим ожиданием М [тх ] = и дисперсией D тх ] —

= (^об /поб ) (Vo6/Vo6 — 2)>

• гамма-распределение 2-го рода для hx:

P(hx/xu…,xn) =

= (vo6/2-l)!eXP{(~Vo6/2)^}{(V°6 /2)^ Г067’"1 (vo6 /2)4

с математическим ожиданием Л/ [А*] = l/^ и дисперсией Z)[Ах] =

= l/[(Vo6/2)(^)2].

Оценка вероятности успешного выполнения задачи. Для фиксиро­ванного числа испытаний п и случайного числа успешных исходов т функция правдоподобия описывается биномиальным распределением:

Р(т/п, R) = — v — Rm(l — R)n~m.

Для данной функции правдоподобия самовоспроизводящимся априорным законом распределения является p-распределение

P(R) = B(y0,40)R*>-l-R)1b- где 5(у0,Ло) = Пуо +Ло’)/ПУо)г(Ло) — Р-функция;

оо

Г(у) = J ху~1 exp{-x}dx — у-функция, которая при целых значениях у о

равна (у-1)!.

Апостериорная плотность вероятности P(R/m, n), полученная после уточнения априорной информации опытными данными по формуле Байеса, представляет собой p-распределение P(R/m, n) = = B(y, r)R?~l(l — R)^- где новые параметры р-распределения опреде­ляются по априорным и экспериментальным данным: у = уо + т т| = rig + л = т.

Выражения для апостериорного математического ожидания и дис­персии имеют вид:

R = у/(у+л); <*2(Я) = Yn/[(Y’l^)2(Y’t^ + l)]-

Для фиксированного числа отказов d и случайного числа испыта­ний до получения заданного числа отказов функция правдоподобия описывается распределением Паскаля:

где q = 1 — R — вероятность невыполнения задачи.

Априорное самовоспроизводящееся распределение для данной функции правдоподобия также представляет собой Р-распределение:

Р(Я)-В(у0, •По)0П°~1(1-«)Го”1-

Все остальные соотношения аналогичны случаю использования биномиального распределения.

Байесовский метод оценивания по точности является оптималь­ным, однако он имеет существенное ограничение: в общем случае байесовские оценки могут быть смещенными. Покажем это на конк­ретном частном примере байесовской оценки вероятности успешного выполнения задачи по частоте. Байесовская оценка вероятности ус­пешного выполнения задачи имеет вид:

^ _ уо+т

1 Уо+Ло+я’

где параметры уд = щ; уд +т|о = пд являются аналогами числа предва­рительных испытаний Пд и числа успешных предварительных испыта­ний ГПд.

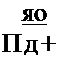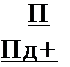Оценка R может быть представлена в виде линейного объедине­ния априорной и экспериментальной информации:

где Rg = ГПд/Пд A, KC = йі/й.

Математическое ожидание этой оценки

Таким образом, байесовская оценка позволяет правильно оце­нить исследуемый показатель только при условии M[Rq] = Л/[ЛэКС] = R.

Полученное условие является условием статистической однород­ности объединяемых априорных и экспериментальных данных, а эф­
фективное применение байесовского метода требует предваритель­ной проверки этого условия. Критерии статистической однородности и соответствующие решающие правила хорошо известны в математи­ческой статистике.

При выполнении условия статистической однородности априор­ных и экспериментальных данных для подтверждения требований к исследуемому показателю R достаточно проведения необходимого объема более простых и дешевых предварительных испытаний. Та­ким образом, целью проведения наиболее сложных и дорогих заклю­чительных испытаний является только проверка статистической од­нородности объединяемых данных. Такая идеология приводит к резкому сокращению объема последних. В табл. 14.2 приведены бай­есовские оценки ряда показателей эффективности.